Single-node Computation#
Introduction#
In this chapter, all base objects (matrices, vectors and stencils) for computation on a single-node (shared-memory) system are described. A typical configuration is illustrated in Fig. 4.
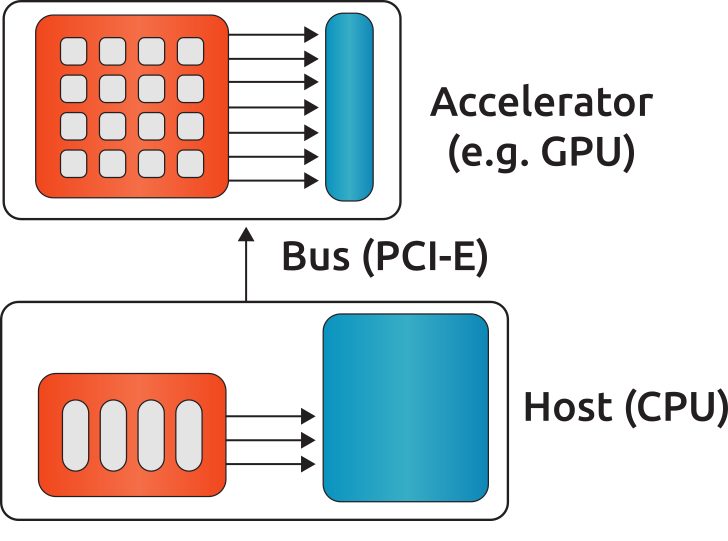
Fig. 4 A typical single-node configuration, where gray boxes represent the cores, blue boxes represent the memory and arrows represent the bandwidth.#
The compute node contains none, one or more accelerators. The compute node could be any kind of shared-memory (single, dual, quad CPU) system.
Note
The host and accelerator memory can be physically different.
ValueType#
The value (data) type of the vectors and the matrices is defined as a template. The matrix can be of type float (32-bit), double (64-bit) and complex (64/128-bit). The vector can be float (32-bit), double (64-bit), complex (64/128-bit) and int (32/64-bit). The information about the precision of the data type is shown in the rocalution::BaseRocalution::Info() function.
Complex Support#
Currently, rocALUTION does not support complex computation.
Allocation and Free#
-
void rocalution::LocalVector::Allocate(std::string name, int64_t size)#
Allocate a local vector with name and size.
The local vector allocation function requires a name of the object (this is only for information purposes) and corresponding size description for vector objects.
- Example
LocalVector<ValueType> vec; vec.Allocate("my vector", 100); vec.Clear();
- Parameters:
name – [in] object name
size – [in] number of elements in the vector
-
virtual void rocalution::LocalVector::Clear()#
Clear (free) the vector.
-
void rocalution::LocalMatrix::AllocateCOO(const std::string &name, int64_t nnz, int64_t nrow, int64_t ncol)#
-
void rocalution::LocalMatrix::AllocateCSR(const std::string &name, int64_t nnz, int64_t nrow, int64_t ncol)#
-
void rocalution::LocalMatrix::AllocateBCSR(const std::string &name, int64_t nnzb, int64_t nrowb, int64_t ncolb, int blockdim)#
-
void rocalution::LocalMatrix::AllocateMCSR(const std::string &name, int64_t nnz, int64_t nrow, int64_t ncol)#
-
void rocalution::LocalMatrix::AllocateELL(const std::string &name, int64_t nnz, int64_t nrow, int64_t ncol, int max_row)#
-
void rocalution::LocalMatrix::AllocateDIA(const std::string &name, int64_t nnz, int64_t nrow, int64_t ncol, int ndiag)#
-
void rocalution::LocalMatrix::AllocateHYB(const std::string &name, int64_t ell_nnz, int64_t coo_nnz, int ell_max_row, int64_t nrow, int64_t ncol)#
-
void rocalution::LocalMatrix::AllocateDENSE(const std::string &name, int64_t nrow, int64_t ncol)#
Allocate a local matrix with name and sizes.
The local matrix allocation functions require a name of the object (this is only for information purposes) and corresponding number of non-zero elements, number of rows and number of columns. Furthermore, depending on the matrix format, additional parameters are required.
- Example
LocalMatrix<ValueType> mat; mat.AllocateCSR("my CSR matrix", 456, 100, 100); mat.Clear(); mat.AllocateCOO("my COO matrix", 200, 100, 100); mat.Clear();
Note
More detailed information on the additional parameters required for matrix allocation is given in Matrix Formats.
-
virtual void rocalution::LocalMatrix::Clear(void)#
Clear (free) the matrix.
Matrix Formats#
Matrices, where most of the elements are equal to zero, are called sparse. In most practical applications, the number of non-zero entries is proportional to the size of the matrix (e.g. typically, if the matrix \(A \in \mathbb{R}^{N \times N}\), then the number of elements are of order \(O(N)\)). To save memory, storing zero entries can be avoided by introducing a structure corresponding to the non-zero elements of the matrix. rocALUTION supports sparse CSR, MCSR, COO, ELL, DIA, HYB and dense matrices (DENSE).
Note
The functionality of every matrix object is different and depends on the matrix format. The CSR format provides the highest support for various functions. For a few operations, an internal conversion is performed, however, for many routines an error message is printed and the program is terminated.
Note
In the current version, some of the conversions are performed on the host (disregarding the actual object allocation - host or accelerator).
// Convert mat to CSR storage format
mat.ConvertToCSR();
// Perform a matrix-vector multiplication y = mat * x in CSR format
mat.Apply(x, &y);
// Convert mat to ELL storage format
mat.ConvertToELL();
// Perform a matrix-vector multiplication y = mat * x in ELL format
mat.Apply(x, &y);
// Convert mat to CSR storage format
mat.ConvertTo(CSR);
// Perform a matrix-vector multiplication y = mat * x in CSR format
mat.Apply(x, &y);
// Convert mat to ELL storage format
mat.ConvertTo(ELL);
// Perform a matrix-vector multiplication y = mat * x in ELL format
mat.Apply(x, &y);
COO storage format#
The most intuitive sparse format is the coordinate format (COO). It represents the non-zero elements of the matrix by their coordinates and requires two index arrays (one for row and one for column indexing) and the values array. A \(m \times n\) matrix is represented by
m |
number of rows (integer). |
n |
number of columns (integer). |
nnz |
number of non-zero elements (integer). |
coo_val |
array of |
coo_row_ind |
array of |
coo_col_ind |
array of |
Note
The COO matrix is expected to be sorted by row indices and column indices per row. Furthermore, each pair of indices should appear only once.
Consider the following \(3 \times 5\) matrix and the corresponding COO structures, with \(m = 3, n = 5\) and \(\text{nnz} = 8\):
where
CSR storage format#
One of the most popular formats in many scientific codes is the compressed sparse row (CSR) format. In this format, instead of row indices, the row offsets to the beginning of each row are stored. Thus, each row elements can be accessed sequentially. However, this format does not allow sequential accessing of the column entries. The CSR storage format represents a \(m \times n\) matrix by
m |
number of rows (integer). |
n |
number of columns (integer). |
nnz |
number of non-zero elements (integer). |
csr_val |
array of |
csr_row_ptr |
array of |
csr_col_ind |
array of |
Note
The CSR matrix is expected to be sorted by column indices within each row. Furthermore, each pair of indices should appear only once.
Consider the following \(3 \times 5\) matrix and the corresponding CSR structures, with \(m = 3, n = 5\) and \(\text{nnz} = 8\):
where
BCSR storage format#
The Block Compressed Sparse Row (BCSR) storage format represents a \((mb \cdot \text{bcsr_dim}) \times (nb \cdot \text{bcsr_dim})\) matrix by
mb |
number of block rows (integer) |
nb |
number of block columns (integer) |
nnzb |
number of non-zero blocks (integer) |
bcsr_val |
array of |
bcsr_row_ptr |
array of |
bcsr_col_ind |
array of |
bcsr_dim |
dimension of each block (integer). |
The BCSR matrix is expected to be sorted by column indices within each row. If \(m\) or \(n\) are not evenly divisible by the block dimension, then zeros are padded to the matrix, such that \(mb = (m + \text{bcsr_dim} - 1) / \text{bcsr_dim}\) and \(nb = (n + \text{bcsr_dim} - 1) / \text{bcsr_dim}\). Consider the following \(4 \times 3\) matrix and the corresponding BCSR structures, with \(\text{bcsr_dim} = 2, mb = 2, nb = 2\) and \(\text{nnzb} = 4\) using zero based indexing and column-major storage:
with the blocks \(A_{ij}\)
such that
with arrays representation
ELL storage format#
The Ellpack-Itpack (ELL) storage format can be seen as a modification of the CSR format without row offset pointers. Instead, a fixed number of elements per row is stored. It represents a \(m \times n\) matrix by
m |
number of rows (integer). |
n |
number of columns (integer). |
ell_width |
maximum number of non-zero elements per row (integer) |
ell_val |
array of |
ell_col_ind |
array of |
Note
The ELL matrix is assumed to be stored in column-major format. Rows with less than ell_width non-zero elements are padded with zeros (ell_val) and \(-1\) (ell_col_ind).
Consider the following \(3 \times 5\) matrix and the corresponding ELL structures, with \(m = 3, n = 5\) and \(\text{ell_width} = 3\):
where
DIA storage format#
If all (or most) of the non-zero entries belong to a few diagonals of the matrix, they can be stored with the corresponding offsets. The values in DIA format are stored as array with size \(D \times N_D\), where \(D\) is the number of diagonals in the matrix and \(N_D\) is the number of elements in the main diagonal. Since not all values in this array are occupied, the not accessible entries are denoted with \(\ast\). They correspond to the offsets in the diagonal array (negative values represent offsets from the beginning of the array). The DIA storage format represents a \(m \times n\) matrix by
m |
number of rows (integer) |
n |
number of columns (integer) |
ndiag |
number of occupied diagonals (integer) |
dia_offset |
array of |
dia_val |
array of |
Consider the following \(5 \times 5\) matrix and the corresponding DIA structures, with \(m = 5, n = 5\) and \(\text{ndiag} = 4\):
where
HYB storage format#
The DIA and ELL formats cannot represent efficiently completely unstructured sparse matrices. To keep the memory footprint low, DIA requires the elements to belong to a few diagonals and ELL needs a fixed number of elements per row. For many applications this is a too strong restriction. A solution to this issue is to represent the more regular part of the matrix in such a format and the remaining part in COO format. The HYB format is a mixture between ELL and COO, where the maximum elements per row for the ELL part is computed by nnz/m. It represents a \(m \times n\) matrix by
m |
number of rows (integer). |
n |
number of columns (integer). |
nnz |
number of non-zero elements of the COO part (integer) |
ell_width |
maximum number of non-zero elements per row of the ELL part (integer) |
ell_val |
array of |
ell_col_ind |
array of |
coo_val |
array of |
coo_row_ind |
array of |
coo_col_ind |
array of |
Memory Usage#
The memory footprint of the different matrix formats is presented in the following table, considering a \(N \times N\) matrix, where the number of non-zero entries is denoted with nnz.
Format |
Structure |
Values |
|---|---|---|
DENSE |
\(N \times N\) |
|
COO |
\(2 \times \text{nnz}\) |
\(\text{nnz}\) |
CSR |
\(N + 1 + \text{nnz}\) |
\(\text{nnz}\) |
ELL |
\(M \times N\) |
\(M \times N\) |
DIA |
\(D\) |
\(D \times N_D\) |
For the ELL matrix \(M\) characterizes the maximal number of non-zero elements per row and for the DIA matrix, \(D\) defines the number of diagonals and \(N_D\) defines the size of the main diagonal.
File I/O#
-
virtual void rocalution::LocalVector::ReadFileASCII(const std::string &filename)#
Read LocalVector from ASCII file.
-
virtual void rocalution::LocalVector::WriteFileASCII(const std::string &filename) const#
Write LocalVector to ASCII file.
-
virtual void rocalution::LocalVector::ReadFileBinary(const std::string &filename)#
Read LocalVector from binary file.
-
virtual void rocalution::LocalVector::WriteFileBinary(const std::string &filename) const#
Write LocalVector to binary file.
-
void rocalution::LocalMatrix::ReadFileMTX(const std::string &filename)#
Read matrix from MTX (Matrix Market Format) file.
Read a matrix from Matrix Market Format file.
- Example
LocalMatrix<ValueType> mat; mat.ReadFileMTX("my_matrix.mtx");
- Parameters:
filename – [in] name of the file containing the MTX data.
-
void rocalution::LocalMatrix::WriteFileMTX(const std::string &filename) const#
Write matrix to MTX (Matrix Market Format) file.
Write a matrix to Matrix Market Format file.
- Example
LocalMatrix<ValueType> mat; // Allocate and fill mat // ... mat.WriteFileMTX("my_matrix.mtx");
- Parameters:
filename – [in] name of the file to write the MTX data to.
-
void rocalution::LocalMatrix::ReadFileCSR(const std::string &filename)#
Read matrix from CSR (rocALUTION binary format) file.
Read a CSR matrix from binary file. For details on the format, see WriteFileCSR().
- Example
LocalMatrix<ValueType> mat; mat.ReadFileCSR("my_matrix.csr");
- Parameters:
filename – [in] name of the file containing the data.
-
void rocalution::LocalMatrix::WriteFileCSR(const std::string &filename) const#
Write CSR matrix to binary file.
Write a CSR matrix to binary file.
The binary format contains a header, the rocALUTION version and the matrix data as follows
// Header out << "#rocALUTION binary csr file" << std::endl; // rocALUTION version out.write((char*)&version, sizeof(int)); // CSR matrix data out.write((char*)&m, sizeof(int)); out.write((char*)&n, sizeof(int)); out.write((char*)&nnz, sizeof(int64_t)); out.write((char*)csr_row_ptr, (m + 1) * sizeof(int)); out.write((char*)csr_col_ind, nnz * sizeof(int)); out.write((char*)csr_val, nnz * sizeof(double));
- Example
LocalMatrix<ValueType> mat; // Allocate and fill mat // ... mat.WriteFileCSR("my_matrix.csr");
Note
Vector values array is always stored in double precision (e.g. double or std::complex<double>).
- Parameters:
filename – [in] name of the file to write the data to.
Access#
Warning
doxygenfunction: Unable to resolve function “rocalution::LocalVector::operator[]” with arguments (int) in doxygen xml output for project “rocALUTION Documentation” from directory: /home/docs/checkouts/readthedocs.org/user_builds/advanced-micro-devices-rocalution/checkouts/docs-6.0.2/docs/.doxygen/docBin/xml. Potential matches:
- ValueType &operator[](int64_t i)
- const ValueType &operator[](int64_t i) const
Warning
doxygenfunction: Unable to resolve function “rocalution::LocalVector::operator[]” with arguments (int) const in doxygen xml output for project “rocALUTION Documentation” from directory: /home/docs/checkouts/readthedocs.org/user_builds/advanced-micro-devices-rocalution/checkouts/docs-6.0.2/docs/.doxygen/docBin/xml. Potential matches:
- ValueType &operator[](int64_t i)
- const ValueType &operator[](int64_t i) const
Note
Accessing elements via the [] operators is slow. Use this for debugging purposes only. There is no direct access to the elements of matrices due to the sparsity structure. Matrices can be imported by a copy function. For CSR matrices, this is rocalution::LocalMatrix::CopyFromCSR() and rocalution::LocalMatrix::CopyToCSR().
// Allocate the CSR matrix
int* csr_row_ptr = new int[100 + 1];
int* csr_col_ind = new int[345];
ValueType* csr_val = new ValueType[345];
// Fill the CSR matrix
// ...
// rocALUTION local matrix object
LocalMatrix<ValueType> mat;
// Import CSR matrix to rocALUTION
mat.AllocateCSR("my_matrix", 345, 100, 100);
mat.CopyFromCSR(csr_row_ptr, csr_col, csr_val);
Raw Access to the Data#
SetDataPtr#
For vector and matrix objects, direct access to the raw data can be obtained via pointers. Already allocated data can be set with SetDataPtr. Setting data pointers will leave the original pointers empty.
-
void rocalution::LocalVector::SetDataPtr(ValueType **ptr, std::string name, int64_t size)#
Initialize a LocalVector on the host with externally allocated data.
SetDataPtrhas direct access to the raw data via pointers. Already allocated data can be set by passing the pointer.- Example
// Allocate vector ValueType* ptr_vec = new ValueType[200]; // Fill vector // ... // rocALUTION local vector object LocalVector<ValueType> vec; // Set the vector data, ptr_vec will become invalid vec.SetDataPtr(&ptr_vec, "my_vector", 200);
Note
Setting data pointer will leave the original pointer empty (set to
NULL).
-
void rocalution::LocalMatrix::SetDataPtrCOO(int **row, int **col, ValueType **val, std::string name, int64_t nnz, int64_t nrow, int64_t ncol)#
-
void rocalution::LocalMatrix::SetDataPtrCSR(PtrType **row_offset, int **col, ValueType **val, std::string name, int64_t nnz, int64_t nrow, int64_t ncol)#
-
void rocalution::LocalMatrix::SetDataPtrMCSR(int **row_offset, int **col, ValueType **val, std::string name, int64_t nnz, int64_t nrow, int64_t ncol)#
-
void rocalution::LocalMatrix::SetDataPtrELL(int **col, ValueType **val, std::string name, int64_t nnz, int64_t nrow, int64_t ncol, int max_row)#
-
void rocalution::LocalMatrix::SetDataPtrDIA(int **offset, ValueType **val, std::string name, int64_t nnz, int64_t nrow, int64_t ncol, int num_diag)#
-
void rocalution::LocalMatrix::SetDataPtrDENSE(ValueType **val, std::string name, int64_t nrow, int64_t ncol)#
Initialize a LocalMatrix on the host with externally allocated data.
SetDataPtrfunctions have direct access to the raw data via pointers. Already allocated data can be set by passing their pointers.- Example
// Allocate a CSR matrix int* csr_row_ptr = new int[100 + 1]; int* csr_col_ind = new int[345]; ValueType* csr_val = new ValueType[345]; // Fill the CSR matrix // ... // rocALUTION local matrix object LocalMatrix<ValueType> mat; // Set the CSR matrix data, csr_row_ptr, csr_col and csr_val pointers become // invalid mat.SetDataPtrCSR(&csr_row_ptr, &csr_col, &csr_val, "my_matrix", 345, 100, 100);
Note
Setting data pointers will leave the original pointers empty (set to
NULL).
LeaveDataPtr#
With LeaveDataPtr, the raw data from the object can be obtained. This will leave the object empty.
-
void rocalution::LocalVector::LeaveDataPtr(ValueType **ptr)#
Leave a LocalVector to host pointers.
LeaveDataPtrhas direct access to the raw data via pointers. A LocalVector object can leave its raw data to a host pointer. This will leave the LocalVector empty.- Example
// rocALUTION local vector object LocalVector<ValueType> vec; // Allocate the vector vec.Allocate("my_vector", 100); // Fill vector // ... ValueType* ptr_vec = NULL; // Get (steal) the data from the vector, this will leave the local vector object empty vec.LeaveDataPtr(&ptr_vec);
-
void rocalution::LocalMatrix::LeaveDataPtrCOO(int **row, int **col, ValueType **val)#
-
void rocalution::LocalMatrix::LeaveDataPtrCSR(PtrType **row_offset, int **col, ValueType **val)#
-
void rocalution::LocalMatrix::LeaveDataPtrMCSR(int **row_offset, int **col, ValueType **val)#
-
void rocalution::LocalMatrix::LeaveDataPtrELL(int **col, ValueType **val, int &max_row)#
-
void rocalution::LocalMatrix::LeaveDataPtrDIA(int **offset, ValueType **val, int &num_diag)#
-
void rocalution::LocalMatrix::LeaveDataPtrDENSE(ValueType **val)#
Leave a LocalMatrix to host pointers.
LeaveDataPtrfunctions have direct access to the raw data via pointers. A LocalMatrix object can leave its raw data to host pointers. This will leave the LocalMatrix empty.- Example
// rocALUTION CSR matrix object LocalMatrix<ValueType> mat; // Allocate the CSR matrix mat.AllocateCSR("my_matrix", 345, 100, 100); // Fill CSR matrix // ... int* csr_row_ptr = NULL; int* csr_col_ind = NULL; ValueType* csr_val = NULL; // Get (steal) the data from the matrix, this will leave the local matrix // object empty mat.LeaveDataPtrCSR(&csr_row_ptr, &csr_col_ind, &csr_val);
Note
If the object is allocated on the host, then the pointers obtained from SetDataPtr and LeaveDataPtr will be on the host. If the vector object is on the accelerator, then the data pointers will be on the accelerator.
Note
If the object is moved to and from the accelerator, then the original pointer will be invalid.
Note
Never rely on old pointers, hidden object movement to and from the accelerator will make them invalid.
Note
Whenever you pass or obtain pointers to/from a rocALUTION object, you need to use the same memory allocation/free functions. Please check the source code for that (for host src/utils/allocate_free.cpp and for HIP src/base/hip/hip_allocate_free.cpp)
Copy CSR Matrix Host Data#
-
void rocalution::LocalMatrix::CopyFromHostCSR(const PtrType *row_offset, const int *col, const ValueType *val, const std::string &name, int64_t nnz, int64_t nrow, int64_t ncol)#
Allocates and copies (imports) a host CSR matrix.
If the CSR matrix data pointers are only accessible as constant, the user can create a LocalMatrix object and pass const CSR host pointers. The LocalMatrix will then be allocated and the data will be copied to the corresponding backend, where the original object was located at.
- Parameters:
row_offset – [in] CSR matrix row offset pointers.
col – [in] CSR matrix column indices.
val – [in] CSR matrix values array.
name – [in] Matrix object name.
nnz – [in] Number of non-zero elements.
nrow – [in] Number of rows.
ncol – [in] Number of columns.
Copy Data#
The user can copy data to and from a local vector by using CopyFromData() CopyToData().
-
void rocalution::LocalVector::CopyFromData(const ValueType *data)#
Copy (import) vector.
Copy (import) vector data that is described in one array (values). The object data has to be allocated with Allocate(), using the corresponding size of the data, first.
- Parameters:
data – [in] data to be imported.
-
void rocalution::LocalVector::CopyToData(ValueType *data) const#
Copy (export) vector.
Copy (export) vector data that is described in one array (values). The output array has to be allocated, using the corresponding size of the data, first. Size can be obtain by GetSize().
- Parameters:
data – [out] exported data.
Object Info#
-
virtual void rocalution::BaseRocalution::Info(void) const = 0#
Print object information.
Infocan print object information about any rocALUTION object. This information consists of object properties and backend data.- Example
mat.Info(); vec.Info();
Copy#
All matrix and vector objects provide a CopyFrom() function. The destination object should have the same size or be empty. In the latter case, the object is allocated at the source platform.
-
virtual void rocalution::LocalVector::CopyFrom(const LocalVector<ValueType> &src)#
Clone the entire vector (values,structure+backend descr) from another LocalVector.
-
void rocalution::LocalMatrix::CopyFrom(const LocalMatrix<ValueType> &src)#
Copy matrix from another LocalMatrix.
CopyFromcopies values and structure from another local matrix. Source and destination matrix should be in the same format.- Example
LocalMatrix<ValueType> mat1, mat2; // Allocate and initialize mat1 and mat2 // ... // Move mat1 to accelerator // mat1.MoveToAccelerator(); // Now, mat1 is on the accelerator (if available) // and mat2 is on the host // Copy mat1 to mat2 (or vice versa) will move data between host and // accelerator backend mat1.CopyFrom(mat2);
Note
This function allows cross platform copying. One of the objects could be allocated on the accelerator backend.
- Parameters:
src – [in] Local matrix where values and structure should be copied from.
Note
For vectors, the user can specify source and destination offsets and thus copy only a part of the whole vector into another vector.
Warning
doxygenfunction: Unable to resolve function “rocalution::LocalVector::CopyFrom” with arguments (const LocalVector<ValueType>&, int, int, int) in doxygen xml output for project “rocALUTION Documentation” from directory: /home/docs/checkouts/readthedocs.org/user_builds/advanced-micro-devices-rocalution/checkouts/docs-6.0.2/docs/.doxygen/docBin/xml. Potential matches:
- void CopyFrom(const LocalVector<ValueType> &src)
- void CopyFrom(const LocalVector<ValueType> &src, int64_t src_offset, int64_t dst_offset, int64_t size)
Clone#
The copy operators allow you to copy the values of the object to another object, without changing the backend specification of the object. In many algorithms, you might need auxiliary vectors or matrices. These objects can be cloned with CloneFrom().
CloneFrom#
-
virtual void rocalution::LocalVector::CloneFrom(const LocalVector<ValueType> &src)#
Clone from another vector.
-
void rocalution::LocalMatrix::CloneFrom(const LocalMatrix<ValueType> &src)#
Clone the matrix.
CloneFromclones the entire matrix, including values, structure and backend descriptor from another LocalMatrix.- Example
LocalMatrix<ValueType> mat; // Allocate and initialize mat (host or accelerator) // ... LocalMatrix<ValueType> tmp; // By cloning mat, tmp will have identical values and structure and will be on // the same backend as mat tmp.CloneFrom(mat);
- Parameters:
src – [in] LocalMatrix to clone from.
CloneBackend#
-
virtual void rocalution::BaseRocalution::CloneBackend(const BaseRocalution<ValueType> &src)#
Clone the Backend descriptor from another object.
With
CloneBackend, the backend can be cloned without copying any data. This is especially useful, if several objects should reside on the same backend, but keep their original data.- Example
LocalVector<ValueType> vec; LocalMatrix<ValueType> mat; // Allocate and initialize vec and mat // ... LocalVector<ValueType> tmp; // By cloning backend, tmp and vec will have the same backend as mat tmp.CloneBackend(mat); vec.CloneBackend(mat); // The following matrix vector multiplication will be performed on the backend // selected in mat mat.Apply(vec, &tmp);
- Parameters:
src – [in] Object, where the backend should be cloned from.
Check#
-
virtual bool rocalution::LocalVector::Check(void) const#
Perform a sanity check of the vector.
Checks, if the vector contains valid data, i.e. if the values are not infinity and not NaN (not a number).
- Return values:
true – if the vector is ok (empty vector is also ok).
false – if there is something wrong with the values.
-
bool rocalution::LocalMatrix::Check(void) const#
Perform a sanity check of the matrix.
Checks, if the matrix contains valid data, i.e. if the values are not infinity and not NaN (not a number) and if the structure of the matrix is correct (e.g. indices cannot be negative, CSR and COO matrices have to be sorted, etc.).
- Return values:
true – if the matrix is ok (empty matrix is also ok).
false – if there is something wrong with the structure or values.
Checks, if the object contains valid data. For vectors, the function checks if the values are not infinity and not NaN (not a number). For matrices, this function checks the values and if the structure of the matrix is correct (e.g. indices cannot be negative, CSR and COO matrices have to be sorted, etc.).
Sort#
-
void rocalution::LocalMatrix::Sort(void)#
Sort the matrix indices.
Sorts the matrix by indices.
For CSR matrices, column values are sorted.
For COO matrices, row indices are sorted.
Keying#
-
void rocalution::LocalMatrix::Key(long int &row_key, long int &col_key, long int &val_key) const#
Compute a unique hash key for the matrix arrays.
Typically, it is hard to compare if two matrices have the same structure (and values). To do so, rocALUTION provides a keying function, that generates three keys, for the row index, column index and values array.
- Parameters:
row_key – [out] row index array key
col_key – [out] column index array key
val_key – [out] values array key
Graph Analyzers#
The following functions are available for analyzing the connectivity in graph of the underlying sparse matrix.
(R)CMK Ordering
Maximal Independent Set
Multi-Coloring
Zero Block Permutation
Connectivity Ordering
All graph analyzing functions return a permutation vector (integer type), which is supposed to be used with the rocalution::LocalMatrix::Permute() and rocalution::LocalMatrix::PermuteBackward() functions in the matrix and vector classes.
Cuthill-McKee Ordering#
-
void rocalution::LocalMatrix::CMK(LocalVector<int> *permutation) const#
Create permutation vector for CMK reordering of the matrix.
The Cuthill-McKee ordering minimize the bandwidth of a given sparse matrix.
- Example
LocalVector<int> cmk; mat.CMK(&cmk); mat.Permute(cmk);
- Parameters:
permutation – [out] permutation vector for CMK reordering
-
void rocalution::LocalMatrix::RCMK(LocalVector<int> *permutation) const#
Create permutation vector for reverse CMK reordering of the matrix.
The Reverse Cuthill-McKee ordering minimize the bandwidth of a given sparse matrix.
- Example
LocalVector<int> rcmk; mat.RCMK(&rcmk); mat.Permute(rcmk);
- Parameters:
permutation – [out] permutation vector for reverse CMK reordering
Maximal Independent Set#
-
void rocalution::LocalMatrix::MaximalIndependentSet(int &size, LocalVector<int> *permutation) const#
Perform maximal independent set decomposition of the matrix.
The Maximal Independent Set algorithm finds a set with maximal size, that contains elements that do not depend on other elements in this set.
- Example
LocalVector<int> mis; int size; mat.MaximalIndependentSet(size, &mis); mat.Permute(mis);
- Parameters:
size – [out] number of independent sets
permutation – [out] permutation vector for maximal independent set reordering
Multi-Coloring#
-
void rocalution::LocalMatrix::MultiColoring(int &num_colors, int **size_colors, LocalVector<int> *permutation) const#
Perform multi-coloring decomposition of the matrix.
The Multi-Coloring algorithm builds a permutation (coloring of the matrix) in a way such that no two adjacent nodes in the sparse matrix have the same color.
- Example
LocalVector<int> mc; int num_colors; int* block_colors = NULL; mat.MultiColoring(num_colors, &block_colors, &mc); mat.Permute(mc);
- Parameters:
num_colors – [out] number of colors
size_colors – [out] pointer to array that holds the number of nodes for each color
permutation – [out] permutation vector for multi-coloring reordering
Zero Block Permutation#
-
void rocalution::LocalMatrix::ZeroBlockPermutation(int &size, LocalVector<int> *permutation) const#
Return a permutation for saddle-point problems (zero diagonal entries)
For Saddle-Point problems, (i.e. matrices with zero diagonal entries), the Zero Block Permutation maps all zero-diagonal elements to the last block of the matrix.
- Example
LocalVector<int> zbp; int size; mat.ZeroBlockPermutation(size, &zbp); mat.Permute(zbp);
- Parameters:
size – [out]
permutation – [out] permutation vector for zero block permutation
Connectivity Ordering#
-
void rocalution::LocalMatrix::ConnectivityOrder(LocalVector<int> *permutation) const#
Create permutation vector for connectivity reordering of the matrix.
Connectivity ordering returns a permutation, that sorts the matrix by non-zero entries per row.
- Example
LocalVector<int> conn; mat.ConnectivityOrder(&conn); mat.Permute(conn);
- Parameters:
permutation – [out] permutation vector for connectivity reordering
Basic Linear Algebra Operations#
For a full list of functions and routines involving operators and vectors, see the API specifications.